Book Review: The Calculus Story

Book: The Calculus Story: A Mathematical Adventure
Author: David Acheson
Pages: 200 (as shown in Kindle app)

I bought the Kindle version and read using Kindle app (not kindle device).

The way this author explained things is absolutely beautiful in a simple to understand format. This author is truly gifted in that sense. The book tries to explain the main ideas in calculus, taking one at a time in a simple way, along with little history of the people involved. I like the way the author slowly introduced each concept.

Calculus is all about the rates at which things change. The subject came fully to life in the 2nd half of the 17th century largely through the work of Isaac Newton, in England, and Gottfried Leibniz, in Germany. Calculus is fundamental to physics and other sciences.

The author provides several interesting results from calculus to appreciate and enjoy calculus purely for their own sake, regardless of any possible practical application. For e.g. look at this interesting connection between pi and the odd numbers!

The above result was first published by Leibniz without any derivation/proof in 1682, but he had discovered it much earlier in about 1674, while working in Paris.

But interestingly, this result was known much earlier by the Indian mathematicians (in Kerala), possibly three centuries before Leibniz and is now often attributed to Madhava, who founded the Kerala school. (their methods were rather different and more highly geometrical).

Before jumping into calculus the author first tell historically different mathematical ideas that slowly evolved one by one starting with one of the earliest geometrical diagram in the Babylonian clay tablet (YBC 7289 at Yale Univ. collection; time period: 1700 BC) which has information about sqrt(2) and its approximate value correct to better than 1 part in million!

The author introduced calculus in this journey, using four main themes:

• the steepness of a curve
• the area enclosed by a curve
• infinite series, and
• the problem of motion

Here is some of the interesting info I noted down during reading:

• while geometry dates back to ancient Greece and beyond, algebra is a much more recent development
• “=” (equal) sign only appeared in 1557, less than a century before Newton was born
• In about 1019, the scholar Al-Biruni estimated the radius of the Earth, obtaining a result which differed from the currently accepted value by less than 1%!!
• infinity enters very early around the time of Archimedes, in about 220 B.C.
• author introduced the idea of “limit” in a beautiful way
• beauty of infinite series: e.g.
  
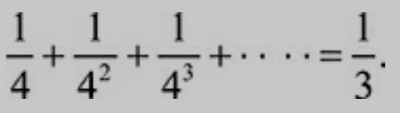
• concept of differentiation
• difference in notation used by Newton and Leibniz
• concept of maximum and minimum (in calculus)
• German astronomer Johannes Kepler discovery
• John Wallis, a Savilian professor of math at Oxford, invented the symbol for infinity
• Wallis discovery in 1655 about a beautiful infinite product:
  
• fundamental theorem of calculus
• In 1643, Evangelista Torricelli, caused quite a sensation by discovering a 3D object that had infinite extent but finite volume!
• if the slices of a spherical loaf of bread are of equal thickness, which piece has the most crust? (ans: they all have the same amount of crust)  This result was known to Archimedes.
• the pizza theorem
• converging/diverging/alternating series
• Leibniz’s paper of 1684
• Marquis l’Hôpital published the first textbook on differential calculus in 1696
• one of the earliest calculus textbooks in English was Charles Hayes’ “A Treatise of Fluxions”, published in 1704
• concept of integration
• who invented calculus? (war between Newton and Leibniz)
• the work of Leonhard Euler (1707-83)
• In 1662, Fermat proposed that light always travels from one given point to another in such a way as to take the least time; Leibniz used his brand new differential calculus to prove this
• the mysterious number: e
• e and Euler
• e and gambling
• e and logarithms
• e and the search for happiness
• calculus with imaginary numbers
• In 1748, Euler took calculus in an altogether different direction with an extraordinary result, linking e with trigonometric functions:
  
• one of the most remarkable equations in the whole of mathematics:
  
• calculus of flight
• playing with infinity is very dangerous
• vanishing trick in dealing with infinite series, was discovered by Bernhard Riemann in 1854
• Fourier series
• calculus and light
• calculus in the quantum world
• calculus goes supersonic
• calculus to chaos theory
• differential equations continue, to this day, to be the most important way in which calculus meets the real world
• pioneering work by Ed Lorenz

I wish all math teacher teach mathematics in a simple way like this author.  The joy of reading this book resulted in, me buying another book by this author: “1809 + All That = A Journey into Mathematics”, which is a small book and I was able to complete in two hours.  That is also a great book.  Will write the review of that book, on another day.

Picture Credit: all pictures are taken from the book.